[PS] 99클럽 코테 스터디 7일차 TIL (하노이의 탑)

문제

문제 링크

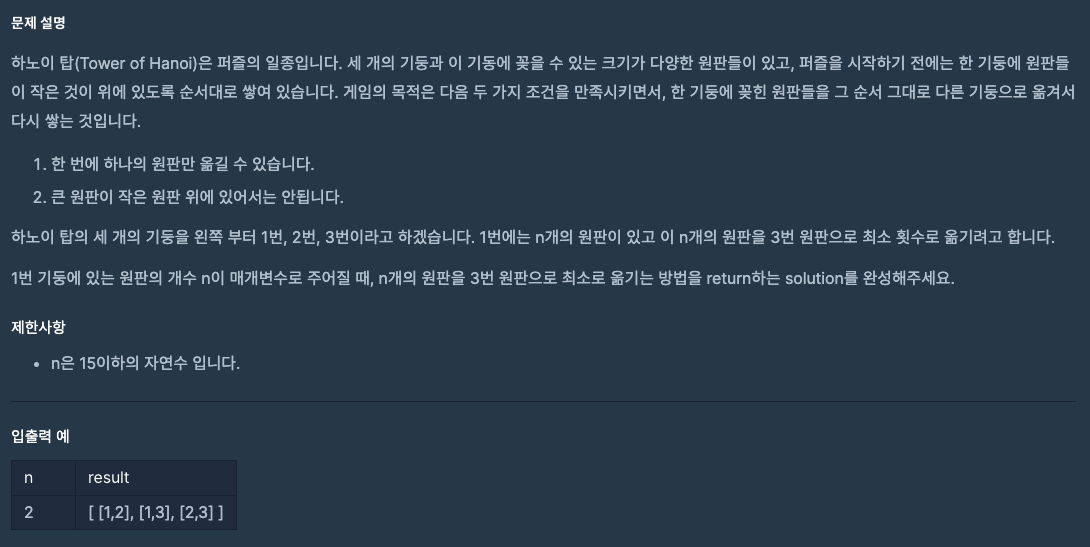
풀이

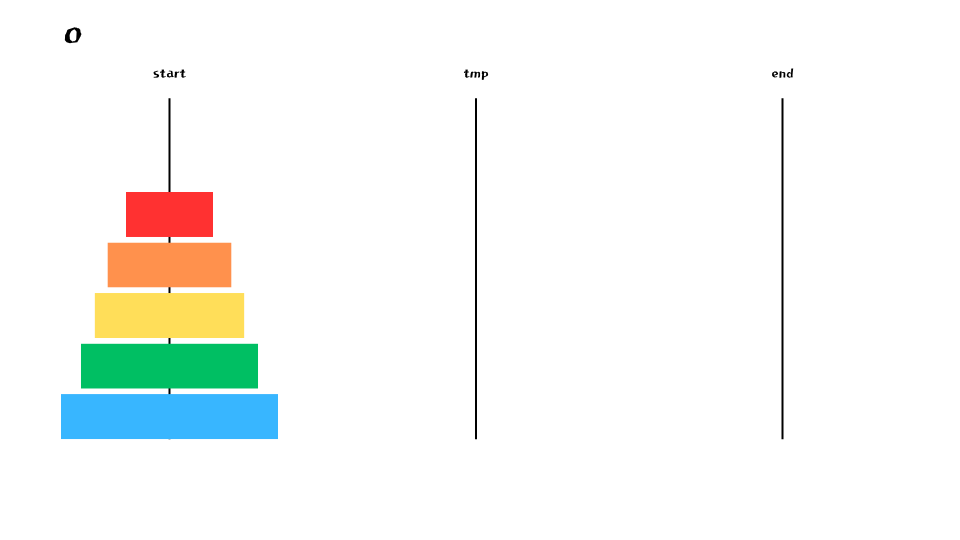
예를들어 n = 5 인 경우 탑을 옮기려면 먼저 맨 아래 원반을 제외한 (n - 1) 개의 원반을 임시 기둥으로 옮겨야 한다. 그 후 맨 아래 원반을 목적지 기둥으로 옮기고, 그 위로 임시 기둥의 원반을 모두 옮기면 된다.

즉, 다음과 같은 단계로 진행해야 한다.

1. (n - 1) 개의 원반을 1번 기둥에서 2번 기둥으로 옮기고,
2. 제일 큰 원반을 1번 기둥에서 3번 기둥으로 옮기고,
3. (n - 1) 개의 원반을 2번 기둥에서 3번 기둥으로 옮긴다.

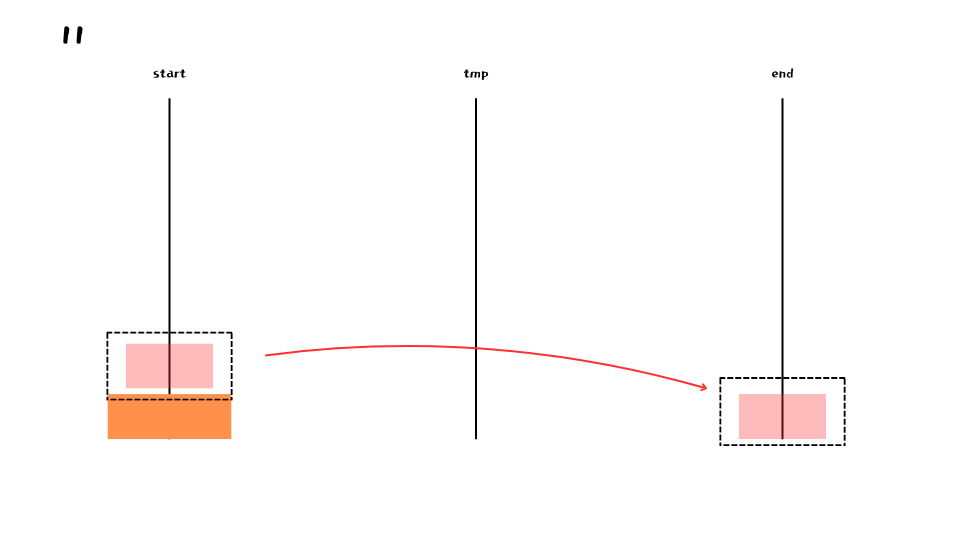
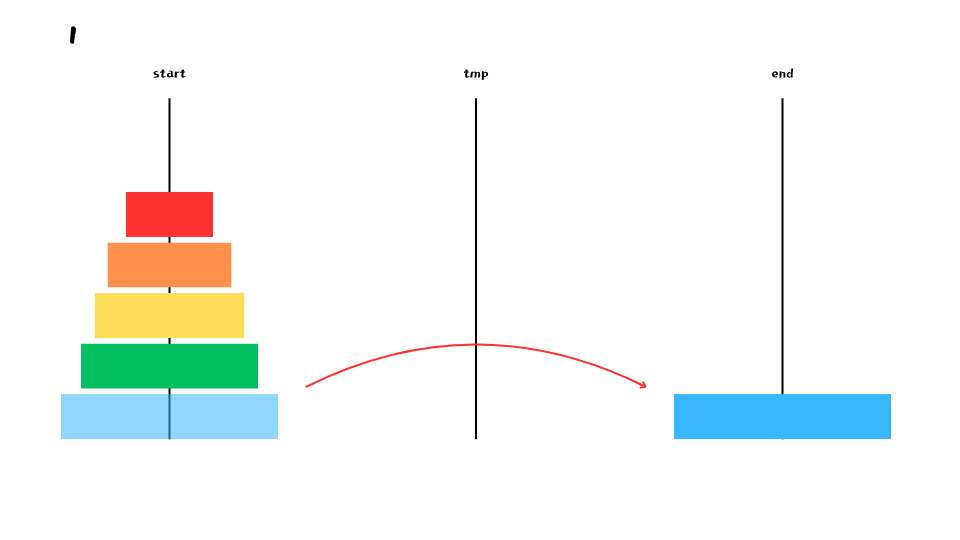맨 아래쪽 원반이 end 쪽으로 가게 하려면 어떻게 해야 될까? 다음 그림처럼 먼저 맨 아래 원반을 제외한 4개의 원반을 tmp 기둥으로 옮겨야 한다.

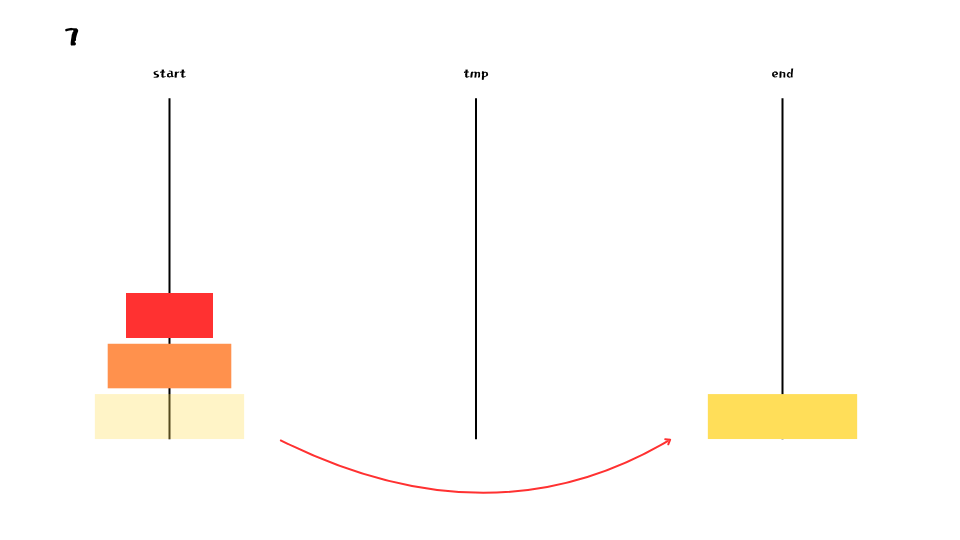
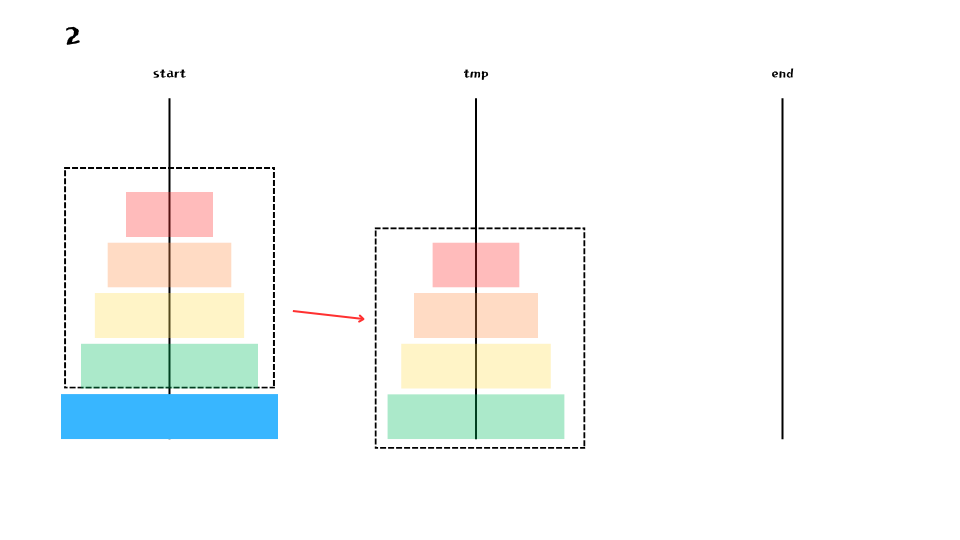4개의 원반을 tmp 로 옮기고 나면 다음 그림과 같이 맨 아래에 있던 원반을 end 로 옮길 수 있게 된다.

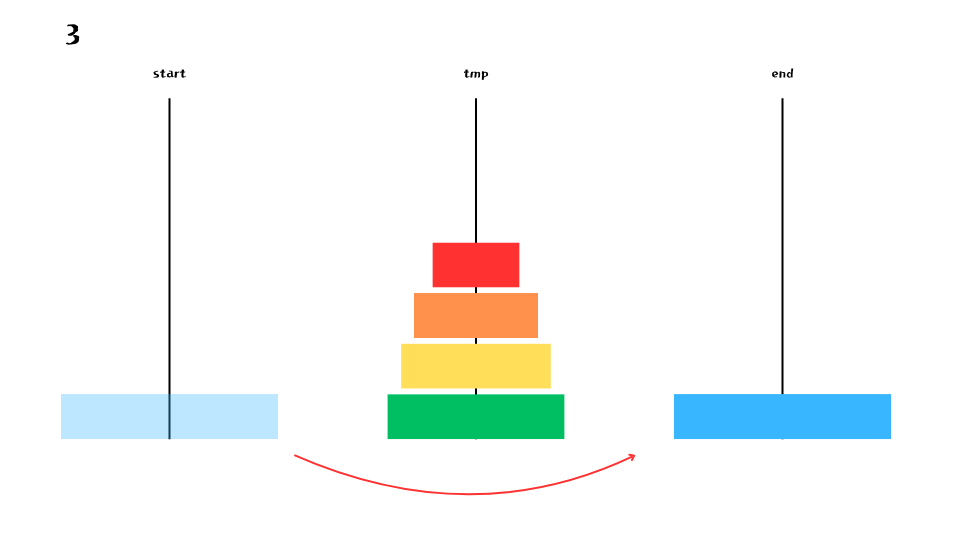지금까지의 과정과 앞으로 진행될 과정을 좀 더 자세히 살펴보면

1. 5개의 원반을 옮기는 과정에 4개의 원반을 옮기는 작업이 선행 되었고,
2. 큰 원반을 end 로 옮기는 작업이 진행되었고,
3. 현재 tmp 에 쌓여 있는 4개의 원반들을 다시 end 로 옮기는 작업이 필요하다.

즉, n = 5의 과정은 n = 4의 과정이 한번 수행된 뒤, 큰 원반을 옮기고, 다시 n = 4의 과정이 수행된다. 다만 그 과정에서 작업이 시작될 기둥(start)과 원반이 모일 기둥(end)의 위치만 변경될 뿐이다.

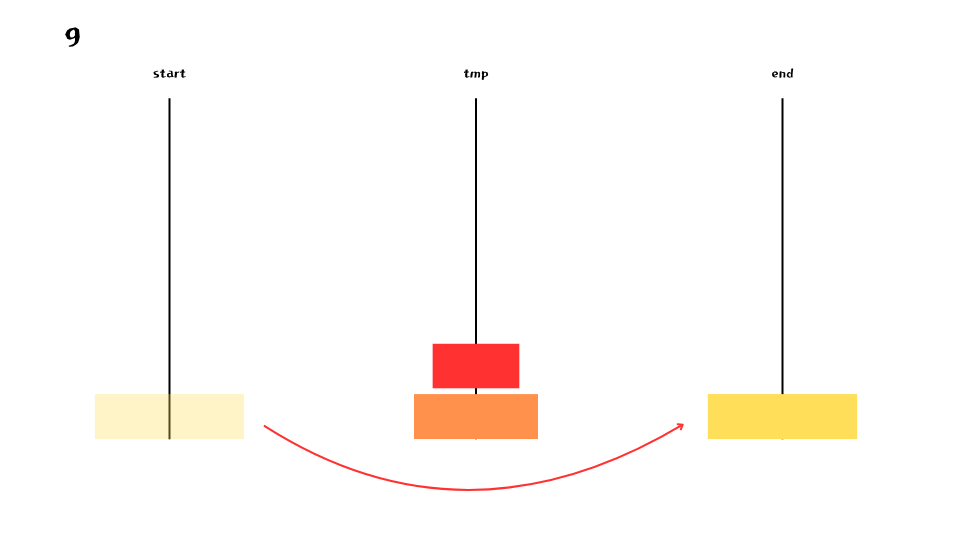
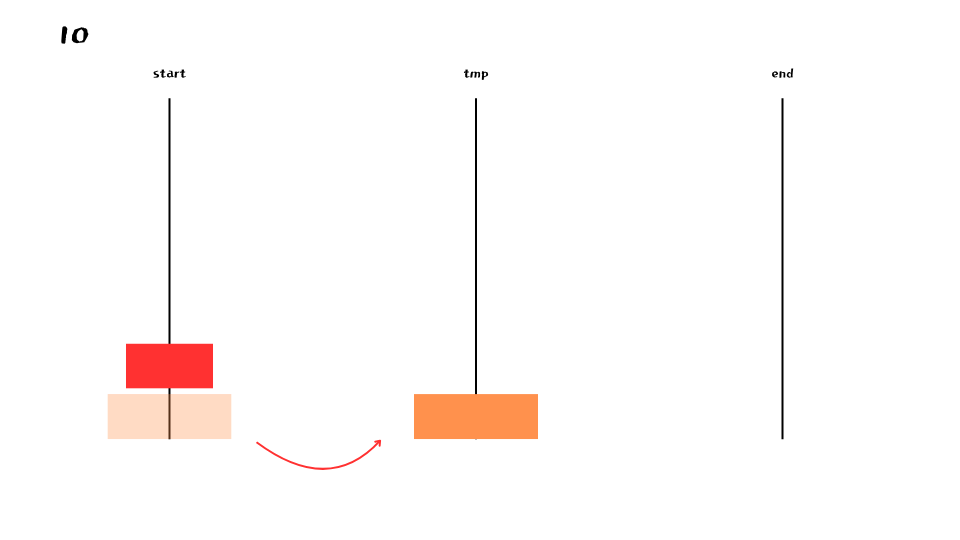
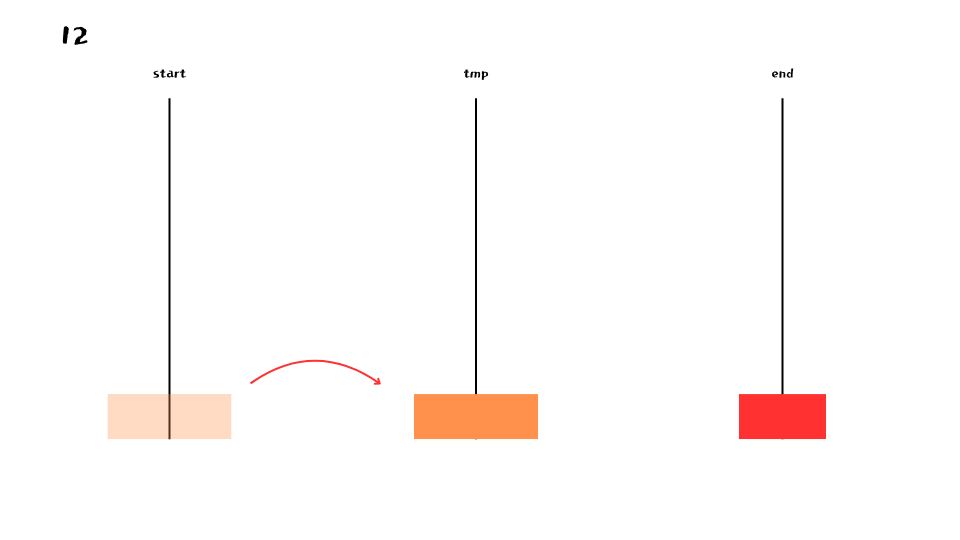
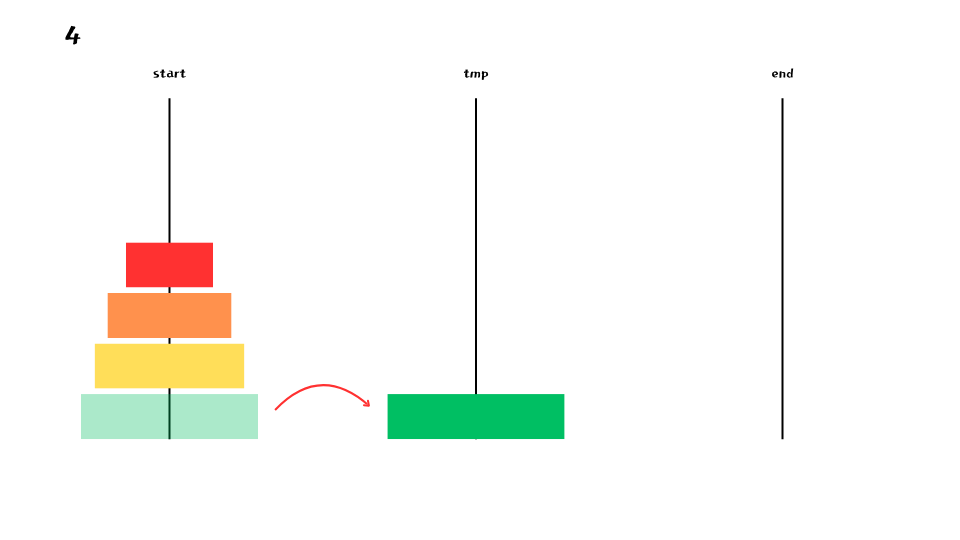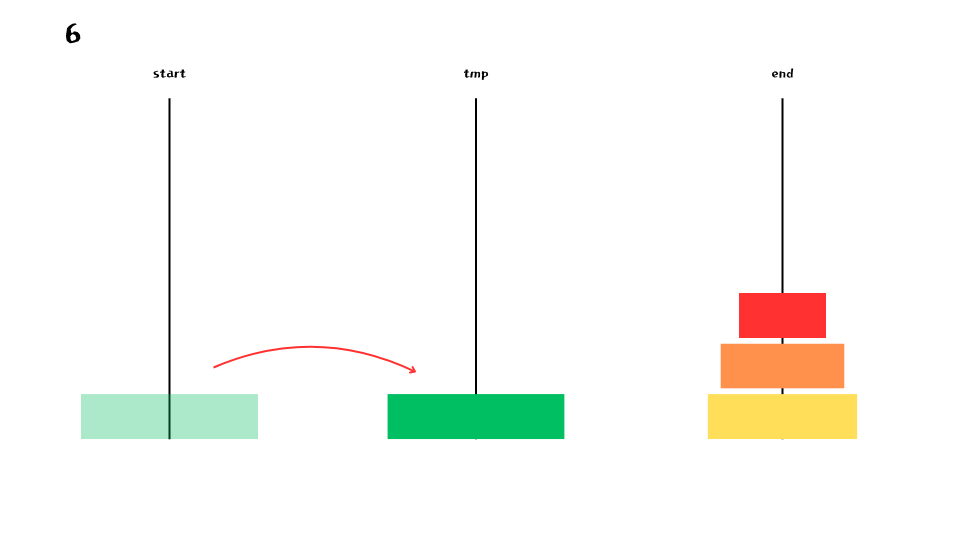
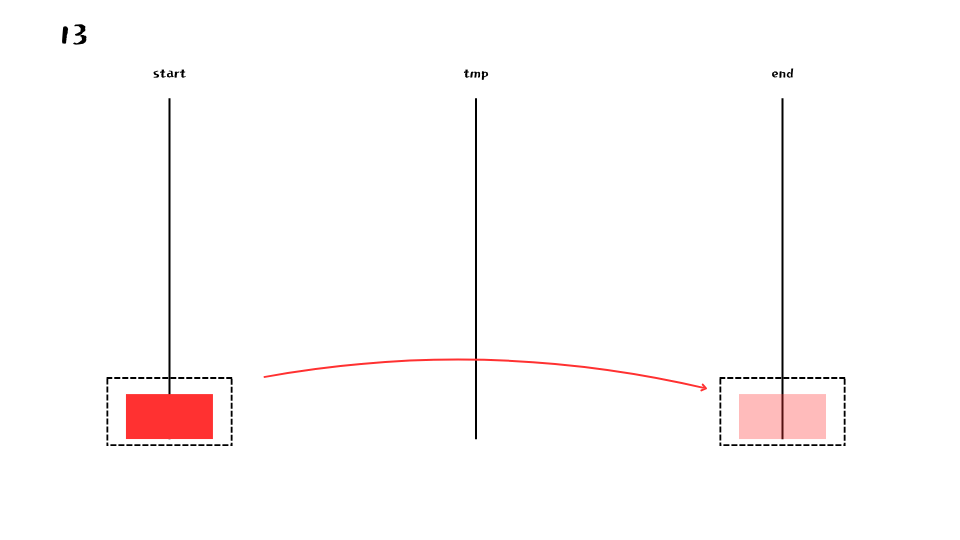
아래는 n = 4 부터 1까지의 대략적인 과정을 나타낸 것이다. 마찬가지로 맨 아래 원반을 제외한 나머지 원반들을 모두 옮기고자 하는 기둥이 아닌 기둥(end) 으로 우선 옮겨야 한다 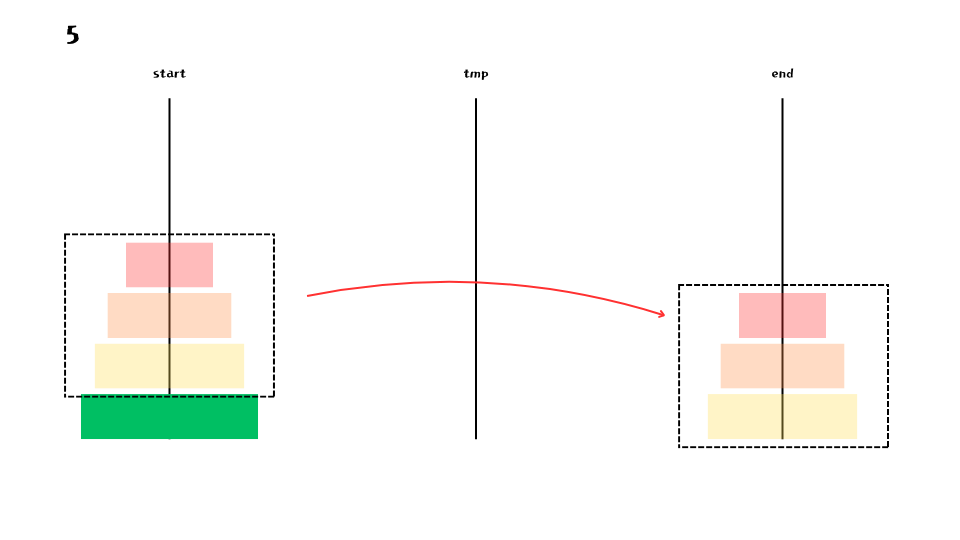이 과정이 n = 1 이 될때 까지 반복 된다.

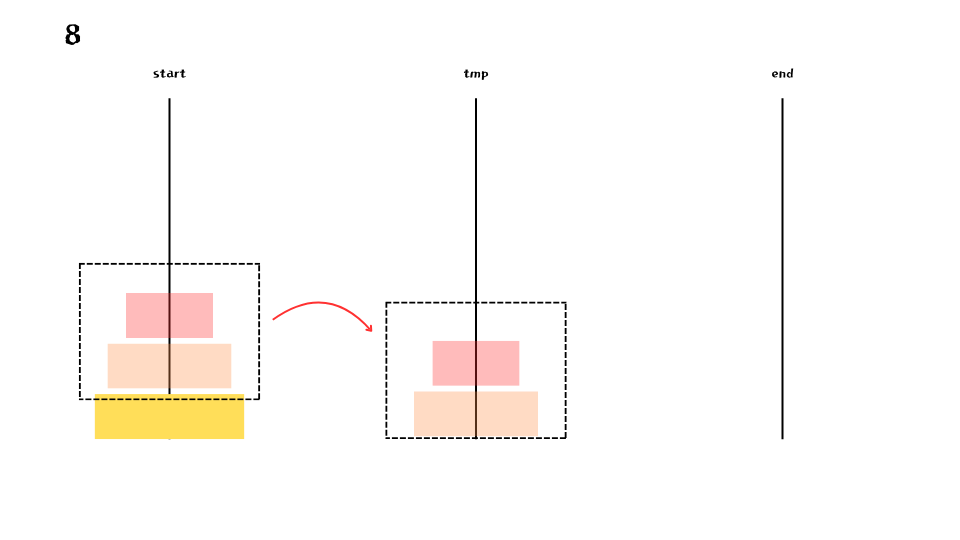
코드

class Solution {
  int index = 0;
  int[][] answer;

  public int[][] solution(int n) {
    answer = new int[(int) (Math.pow(2, n) - 1)][2];
    hanoi(n, 1, 3, 2);

    return answer;
  }

  void hanoi(int n, int start, int end, int tmp) {
    if (n == 1) {
      record(start, end);
      return;
    }
    hanoi(n-1, start, tmp, end);   // 1
    record(start, end);            // 2
    hanoi(n-1, tmp, end, start);   // 3
  }

  void record(int start, int end) {
    answer[index][0] = start;
    answer[index][1] = end;
    index++;
  }
}

• 코드의 1번 부분이 위 3번 그림에 해당한다. n 이 5일때 코드의 1번 부분은 4번 실행되고 tmp 에 4개의 원반이 쌓여 있을 것이다.
• 코드의 2번 부분이 큰 원반을 start 에서 end 로 이동하는 부분이다. 배열에 시작 위치와 끝 위치를 기록해 둔다.
• 코드의 3번 부분이 tmp 에 있는 4개의 원반을 end 로 이동하는 부분이다. n = 1 이 되면 1개의 원반만 옮기면 되기 때문에 바로 배열에 이동경로를 기록해준다.

그리고 answer 배열의 크기가 곧 최소 이동 횟수 인데, 다음과 같은 과정을 통해 알 수 있다.

hanoi(n) : n 개의 원반을 옮기는데 필요한 이동 횟수

hanoi(n) = hanoi(n-1) * 2 + 1

// 양변에 + 1
hanoi(n) + 1 = 2 * (hanoi(n-1) + 1)
hanoi(n-1) + 1 = 2 * (hanoi(n-2) + 1)
hanoi(n-2) + 1 = 2 * (hanoi(n-3) + 1)
  ...
hanoi(2) + 1 = 2 * (honoi(1) + 1)

// 좌변과 우변을 곱한다.
(hanoi(n) + 1) * (hanoi(n-1) + 1)...(hanoi(2) + 1) = 2^(n-1) * (hanoi(n-1) + 1) * (hanoi(n-2) + 1)...(hanoi(1) + 1)

// 공통 부분 나눈다.
(hanoi(n) + 1) = 2^(n-1) * (hanoi(1) + 1)
  
// hanoi(1) = 1 대입
(hanoi(n) + 1) = 2^(n-1) * 2

hanoi(n) = 2^n -1

참고

https://shoark7.github.io/programming/algorithm/tower-of-hanoi