[PS] 99클럽 코테 스터디 33일차 TIL (리코쳇 로봇)

문제

문제 링크

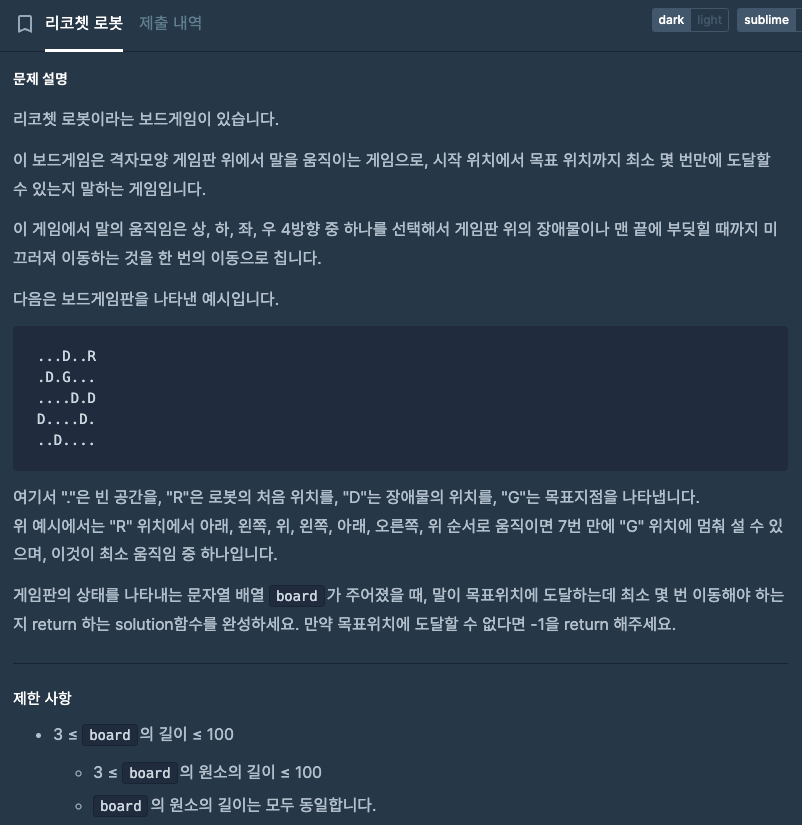
설명

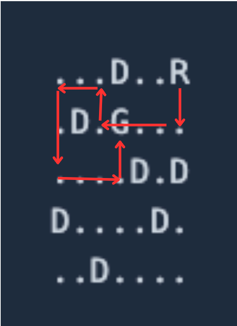
위 그림처럼 “R” 에서 출발해 상하좌우로 움직일 수 있는데 이전까지 풀어봤던 BFS/DFS 문제와 다른점은 한 칸씩 움직이면서 상하좌우를 탐색해가는 방식이 아니라

• “D” 를 만날때 까지 움직이거나
• 격자의 끝 부분을 만날때 까지 움직인다.

예시의 경우 빨간 화살표 대로 총 7번 움직이면 “R” 에서 “G” 까지 갈 수 있는 최단 경로가 된다.

풀이

이전까지의 문제는 주로 DFS 로 풀었는데 이번 문제는 BFS 로 푸는 것이 더 적절하다. DFS 로 푸는 경우 최단 경로인지 확인하는 로직이 추가로 필요하다.

탐색을 시작할 “R” 의 위치를 찾은 후 BFS 를 시작한다. bfs 함수에서는 “R” 에서 출발해 “G” 에 도달할 때 까지의 정점 간의 거리를 구해주면 된다. 정점 간의 거리를 구할 땐 dist 변수를 dfs 함수의 인자로 전달하거나 bfs 의 경우 queue 에 넣어주는 식으로 구하면 된다.

장애물을 만나거나 벽에 도달할때 까지 쭉 이동한 후, 그 노드가 아직 방문 전이라면 방문처리를 해주고 다음 탐색을 위해 queue 에 좌표를 넣어준다. 이때, dist + 1 을 넘겨줘서 노드 간 이동 거리를 계산해 준다.

class Solution {
  static String[][] graph;
  static boolean[][] visited;
  static int[] dx = {-1, 1, 0, 0};
  static int[] dy = {0, 0, -1, 1};
  static int n;

  public int solution(String[] board) {
    n = board.length;
    graph = new String[n][];
    visited = new boolean[n][];

    int x = 0, y = 0;
    for (int i = 0; i < n; i++) {
      graph[i] = new String[board[i].length()];
      visited[i] = new boolean[board[i].length()];
      char[] charArray = board[i].toCharArray();
      for (int j = 0; j < charArray.length; j++) {
        String s = String.valueOf(charArray[j]);
        graph[i][j] = s;
        if (s.equals("R")) {
          x = i;
          y = j;
        }
      }
    }
    return bfs(x, y);
  }

  private int bfs(int x, int y) {
    Queue<int[]> queue = new LinkedList<>();
    queue.add(new int[] {x, y, 0});
    visited[x][y] = true;

    while (!queue.isEmpty()) {
      int[] current = queue.poll();
      int cx = current[0];
      int cy = current[1];
      int dist = current[2];

      if (graph[cx][cy].equals("G")) {
        return dist;
      }

      for (int i = 0; i < 4; i++) {
        int nx = cx;
        int ny = cy;

        while (isInRange(nx + dx[i], ny + dy[i]) && !graph[nx + dx[i]][ny + dy[i]].equals("D")) {
          nx += dx[i];
          ny += dy[i];
        }

        if (!visited[nx][ny]) {
          visited[nx][ny] = true;
          queue.add(new int[] {nx, ny, dist + 1});
        }
      }
    }
    return -1;
  }

  private boolean isInRange(int x, int y) {
    return x >= 0 && x < n && y >= 0 && y < graph[x].length;
  }
}