[PS] 99클럽 코테 스터디 32일차 TIL (무인도 여행)

문제

문제 링크

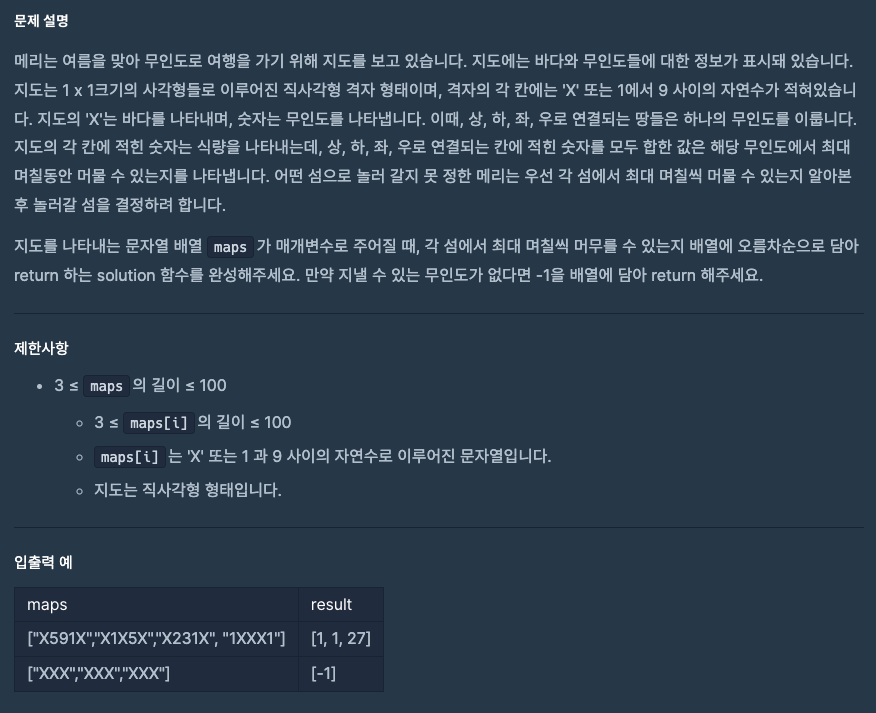
입출력 예

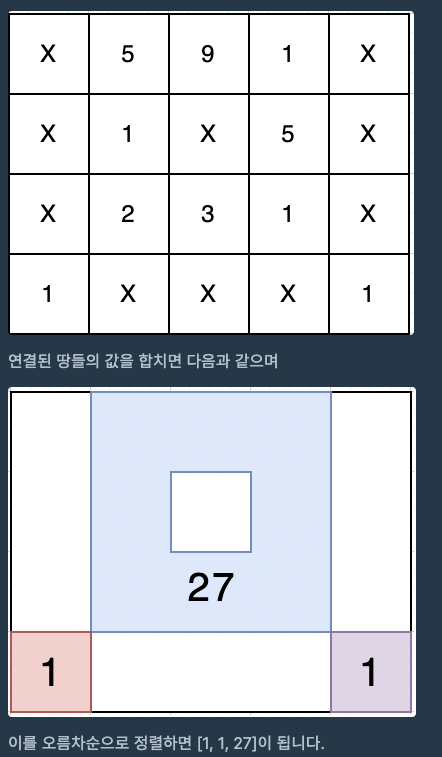
설명

지도 정보가 배열로 주어지는데, 각 영역엔 숫자가 적혀있거나, “X” 표시가 있다. 탐색하는 영역의 숫자를 합친 배열을 반환하면 된다.

풀이

그래프의 모든 정점이 주어지므로, 이를 나타내기 위해 그래프를 2차원 배열로 선언한다. 그 후 배열의 첫번째 인덱스부터 상하좌우 모든 방면으로 탐색해가면서 그 정점에 적힌 수를 합친 배열을 반환해야 한다. 그래프에서 각 정점에 적힌 수는 graph[x][y] 로 알 수 있다. dfs 시작 정점부터 탐색할때마다 이 값을 누적한 값을 반환하고, list 에 저장한다. 오름차순 정렬 후 배열로 반환한다.

전체 코드 중 제일 핵심적인 코드는 size += dfs(nx, ny) 이 코드라고 할 수 있다.

class Solution {
  static String[][] graph;
  static boolean[][] visited;
  static int n;
  static int[] dx = {-1, 1, 0, 0};
  static int[] dy = {0, 0, -1, 1};
  static ArrayList<Integer> answer = new ArrayList<>();

  public int[] solution(String[] maps) {
    n = maps.length;
    graph = new String[n][];
    visited = new boolean[n][];

    for (int i = 0; i < n; i++) {
      graph[i] = new String[maps[i].length()];
      visited[i] = new boolean[maps[i].length()];
      char[] charArray = maps[i].toCharArray();
      for (int j = 0; j < charArray.length; j++) {
        graph[i][j] = String.valueOf(charArray[j]);
      }
    }

    for (int x = 0; x < n; x++) {
      for (int y = 0; y < graph[x].length; y++) {
        if (!visited[x][y] && !graph[x][y].equals("X")) {
          answer.add(dfs(x, y));
        }
      }
    }

    if (answer.isEmpty()) {
      return new int[] {-1};
    }

    return answer.stream().mapToInt(Integer::intValue).sorted().toArray();
  }

  private static int dfs(int x, int y) {
    visited[x][y] = true;
    int size = Integer.parseInt(graph[x][y]);

    for (int i = 0; i < 4; i++) {
      int nx = x + dx[i];
      int ny = y + dy[i];

      if (isInRange(nx, ny) && !visited[nx][ny] && !graph[nx][ny].equals("X")) {
        size += dfs(nx, ny);
      }
    }
    return size;
  }

  private static boolean isInRange(int x, int y) {
    return x >= 0 && x < n && y >= 0 && y < graph[x].length;
  }
}