[CS] 데이터 저장 방식 - 정수(Integer)

✔️ 컴퓨터의 데이터 저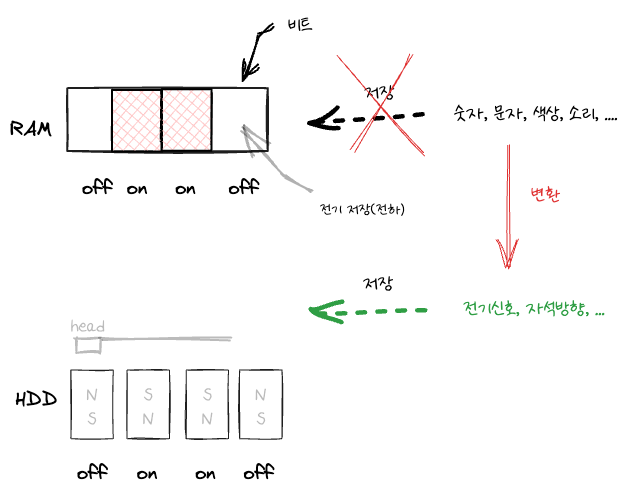장 방식

저장방식

• 전기적/마그네틱 신호로 의미를 전달할 수 있는 가장 간단한 방식이 ON/OFF 방식이다.
• 이를 표현하기 가장 적절한 방식이 2진법이다.
• 하나의 비트는 0이나 1의 값을 가질 수 있고, 각각은 참, 거짓 혹은 서로 배타적인 상태를 나타낸다.
• 따라서 값을 메모리에 저장하려면 데이터를 2진수로 표현할 수 있어야 한다.
  • 문자같은 경우 charset 에 의해 변환된다.
• 적은 메모리로 더 많은 상태를 관리할 수 있다. (1bit 당 두 가지의 상태를 표현할 수 있다.)
• 메모리 기본 단위 : 8bit == 1byte

  예시로 들자면, 인간은 손가락이 몇 개 펴져있는지, 혹은 접혀있는지를 센다면, 기계는 손가락에 특정 순서를 할당하여 몇 번째 손가락이 펴지고 접혔는지를 파악하여 그것을 숫자로 인식하는 식이다. 해당 부분은 비트 연산의 응용 부분에서 좀 더 자세히 다뤄보겠다.

✔️ 비트 크기와 저장할 수 있는 값의 범위

8bit (255)

• 00000000 ~ 11111111 (-128 ~ +127)
• 맨 앞에 0 을 붙인다.

16bit (65535)

• \(-2^{15}\) ~ \(2^{15}\) (-32,768 ~ 32,767)
• 맨 앞에 0x 를 붙인다.

32bit (약 42억)

• 약 -21억 ~ + 21억

💡 예를 들어 22억 이라는 돈의 액수를 저장하려고 하면, 최소 64bit(8byte) 메모리가 필요하다.

bit	단위
8bit(1byte)	byte
16bit(2byte)	short
32bit(4byte)	int
64bit(8byte)	long

✔️ 정수를 2진수로 표현하는 방법

부호-크기/절대값(Sign-Magnitude)

• 부동 소수점에서 가수부(significand or mantissa)를 저장할 때 사용한다.
• 맨 왼쪽 1비트를 부호 비트로 사용한다. 양수는 0, 음수는 1 이다.
• 나머지 비트는 절대값(magnitude)으로 저장한다.
  • 8비트 = 1비트(부호) + 7비트(절대값, 크기)

       ex) +24 => |+24| = 24 ---> 0001 1000
       ex) -24 => |-24| = 24 ---> 1001 1000
    

• 수의 범위(8비트 기준): -127 ~ + 127

   0111 1111 (127)
   0111 1110 (126)
   0111 1101 (125)
      ...
   0000 0001 (1)
   0000 0000 (+0)   
   1000 0000 (-0) 
   1000 0001 (-1)
      ...
   1111 1101 (-125)
   1111 1110 (-126)
   1111 1111 (-127)
  

• 단점
  • 두 개의 0(+0, -0)이 존재한다.
  • 양수와 음수를 더했을 때 옳지 않은 값이 나온다.

     ex) 4비트일 경우, 1 + -1 = ?
         0001(+1) + 1001(-1) = 1010 (-2) <-- 계산 결과가 옳지 않다.
  

  • 빼기를 처리하는 컴퓨팅 회로를 별도로 설계해야 하므로 하드웨어가 복잡해진다.
• 장점
  • 이해하기 쉽다!

1의 보수(Signed 1’s Complement)

• Sign-Magnitude 방식에서는 부호(+,-)표시를 맨 앞의 1비트를 이용해서 표시했다. 그러나 이런 방식으로는 제대로 된 연산이 힘들었고, 결국 새로운 부호 표시 방법을 찾게된다.
• 가산기(adder)를 사용하는 컴퓨터가 음의 정수를 표현하기 위해선 아래와 같은 아이디어가 필요하다.

  •   A-B = A+(-B)
    

    예를들어 주판을 이용한 덧셈, 뺄셈 시에 5, 10의 보수를 사용한다. 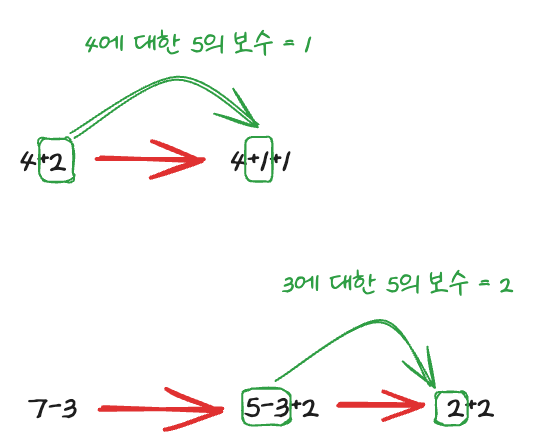보수 생각 해보면 평소 10진수 뺄셈을 할때 보수를 이용해 뺄셈을 하고 있다. 14-6 을 계산할 때 4+4 로 계산 하는 것과 같다.

• ex) 14-6 
      => 10+4-6 => -6을 하는것이 아니라, 6에 대한 10의 보수인 4를 더한다. 
      => 4+4
  

• 제한된 자릿수의 정수만을 사용할 때는 음수를 표현할 때 음의 부호 표현을 사용하는 대신 보수를 이용한 표현을 사용할 수 있다.

1의 보수로 바꾸는 방법(XOR연산)

• 모든 비트를 반대로 뒤집는다.

    8bit 기준
    ex) +24 => 0001 1000
    ex) -24 => 1110 0111

• 수의 범위(8비트 기준): -127 ~ +127

     0111 1111 (127)
     0111 1110 (126)
     0111 1101 (125)
        ...
     0000 0001 (1)
     0000 0000 (+0)
     1111 1111 (-0)
     1111 1110 (-1)
        ...
     1000 0010 (-125)
     1000 0001 (-126)
     1000 0000 (-127)

연산

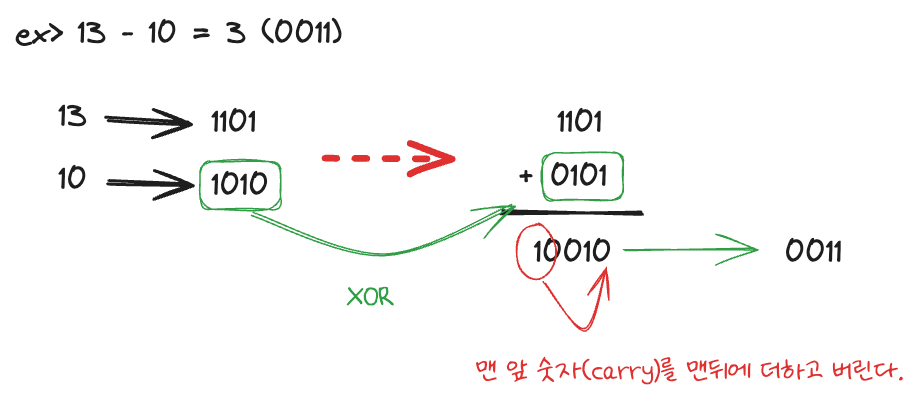1의 보수 연산

• 여전히 두 개의 0(+0, -0)이 존재한다.
• 두 수를 더한 후 비트 크기를 초과한 1 값(carry)을 다시 맨 뒤에 더해야만 옳은 값이 된다.

✍️ 보수(補數) 란 보수(補數)는 보충을 해주는 수를 의미한다. 이를테면 1에 대한 10의 보수는 9, 4에 대한 15의 보수는 11의 개념이다. 1에 대한 2의 보수는 1이다.

2의 보수(Signed 2’s Complement)

• 1의보수에 1을 더한 값.
• 자바에서 음수를 저장하는 방법.
• 1의 보수의 문제점을 해결하기 위해 등장한 방법. (계산 후 1을 더하는 것이 아닌, 미리 1을 더해놓고 계산)
• 음수 0을 없앰으로써 -128까지 표현할 수 있다.

2의 보수로 바꾸는 방법

case 1) 모든 비트를 반대 값(1의 보수)으로 만든 다음 1을 더한다.

   ex) 0010 1001(+41)
       1101 0110(1의 보수)
     +         1
      -----------
       1101 0111(-41)

case 2) 오른쪽에서부터 1을 찾는다.

• 찾은 1의 왼쪽편에 있는 모든 비트를 반대 값으로 바꾼다.

    ex) 0010 1001(41) => 1101 0111(-41)
                ^                ^
    ex) 0010 1100(44) => 1101 0100(-44)
                ^                ^

• 수의 범위(8비트 기준): -128 ~ +127

     0111 1111 (127)
     0111 1110 (126)
     0111 1101 (125)
        ...
     0000 0010 (2)
     0000 0001 (1)
     0000 0000 (+0)
     1111 1111 (-1)
     1111 1110 (-2)
        ...
     1000 0011 (-125)
     1000 0010 (-126)
     1000 0001 (-127)
     1000 0000 (-128)

연산

  ex) 10 - 7 = 10 + (-7) = 3
      10      => 0000 1010
      7       => 0000 0111
      -7      => 1111 1000 + 1 = 1111 1001

      0000 1010 (10)
    + 1111 1001 (-7)
    -----------------
    1 0000 0011 (3)  => 8비트를 넘어가는 값은 버린다.

• 장점
  • 양수와 음수의 덧셈이 가능하다. –> 덧셈으로 빼기를 수행할 수 있다.
  • 음수 0이 없다. 0에 대한 표현이 한 가지이다.

K-초과 (Excess-K)

• 부동 소수점의 지수부(exponent)를 저장할 때 사용한다.
• 오프셋 바이너리(offset binary) 또는 바이어스된 표기법(biased representation) 이라고도 한다.
• K를 바이어스 값이라 부르며, 표현하려는 값에 더할 때 사용한다.
  표현하려는 값 + 초과 값(K) = 결과

• 바이어스 값(K)을 구하는 공식: K = \(2^{비트수 - 1}\)

  ex) 8비트일 경우 —> K = \(2^{8 - 1}\) = \(2^7\) = 128,

      결과 = 128 + 값
  
    1111 1111 = 128 + 127
    1111 1110 = 128 + 126
    1111 1101 = 128 + 125
    ...
    1000 0001 = 128 + 1
    1000 0000 = 128 + 0
    0111 1111 = 128 + (-1)
    ...
    0000 0010 = 128 + (-126)
    0000 0001 = 128 + (-127)
    0000 0000 = 128 + (-128)
  

IEEE-754 부동소수점 표준

• K = \(2^{비트수 - 1}\) - 1

  ex) 8비트일 경우 —> K = \(2^7\) - 1 = 127,

      결과 = 127 + 값

    1111 1111 = 127 + 128
    1111 1110 = 127 + 127
    1111 1101 = 127 + 126
    1111 1100 = 127 + 125
    ...
    1000 0000 = 127 + 1
    0111 1111 = 127 + 0
    0111 1110 = 127 + (-1)
    ...
    0000 0010 = 127 + (-125)
    0000 0001 = 127 + (-126)
    0000 0000 = 127 + (-127)

바이어스 방식(Excess-K, IEEE-754)으로 데이터를 저장할 때의 이점?

• 모든 비트가 0일 때 최소 값을 가지고, 모든 비트가 1일 때 최대 값을 갖는다.
• 이런 이유로 작은 값에서 큰 값으로 정렬되는 결과를 낳는다.
• 모든 비트가 정렬된 상태이기 때문에 부동소수점이든 정수이든 상관없이 값을 비교할 때 속도가 빠르다.
• 부호-크기, 1의 보수, 2의 보수와 같은 방법으로 값을 표현할 경우, 비트들이 순차적으로 정렬되지 않는다.

정리

컴퓨터가 정수형 데이터를 어떤식으로 저장하는지에 대해 알아보았습니다. 다음 포스트에서는 실수(부동소수점)를 저장하는 방식에 대해 알아봅니다.

reference

• https://ndb796.tistory.com/4
• https://ko.wikipedia.org/wiki/보수_(수학)