[CS] 데이터 저장 방식 - 실수(Real number)

이전 글 에서 정수의 저장 방법에 대해 살펴봤습니다. 이번 글에서는 실수를 2진수로 나타내는 방법에 대해 알아보겠습니다.

✔️ 실수를 2진수로 표현하는 방법

부동소수점에 대해 알아보기 전에 10진수 정수를 2진수로 변환하는 과정을 다시 살펴보자.
\(13_{(10)}\) 을 2진수로 바꾸기 위해 다음과 같이 2로 계속해서 나눈다. 여기서 나눈다는 행위의 의미는 2가 13에 몇개나 포함되어 있는지를 알아보기 위함이다. 10진수가 10이 될 때 마다 자릿 수가 올라가듯이 2진수 에서는 2가 될때 자릿 수가 하나 올라가기 때문이다.

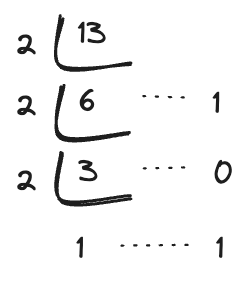13을 2진수로 바꾸는 과정

위처럼 나눗셈 후 나머지를 아래에서부터 순서대로 위로 나열하면 1101이 되고 이게 13의 2진수가 된다.
왜 그렇게 되는지 한 눈에 알아보기 쉽게 곱하기 형식으로 바꿔보겠다.

우선 13에 2가 몇개 들어있는지 알기 위해선 \(2^n\) 형식으로 나타내야 한다. 이때, 나눗셈 정리를 이용해 곱의 형태로 표현해보면 아래처럼 2의 거듭제곱으로 표현할 수 있다.

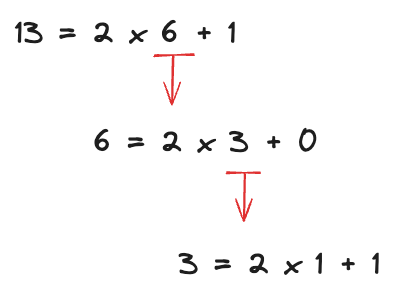나눗셈 정리

\[\begin{align} 13 &= 2 \cdot (2 \cdot (2 \cdot 1 + 1) + 0) + 1 \cr &= 2 \cdot (2 \cdot ( 2 + 1 ) + 0) + 1 \cr &= 2 \cdot ( 2^2 + 2^1 + 0) + 1 \cr &= 2^3 + 2^2 + 2^0 \end{align} \]

\[ 2^3 \times \color{red} 1 \color{black} + 2^2 \times \color{red} 1 \color{black} + 2^1 \times \color{red} 0 \color{black} + 2^0 \times \color{red} 1 \color{black} = 1101_2 \]

정수의 경우 10진수를 2로 계속 나누면서 1 또는 0을 뽑아내 아래에서부터 순서대로 나열하면 2진수가 된다. 이는 2진수 변환 과정에서 \(2^n\) 자리 비트를 채워가는 과정이라고 보면 될 것 같다.

그러면 정수가 아니라 실수(real number)의 경우 소수 부분은 어떻게 처리해야 할까?

예를들어 가격이 1200원인 물건을 구매하려고 한다. 이때 2000원을 낸다면 거스름돈을 구하는 과정을 생각해보자. 당연히 단위가 큰 지폐부터 차례대로 몇장이 필요한지 생각할 것이다.
2진수로 변환하는 과정도 똑같다.

정수 부분의 제일 큰 단위인 \(2^n\) 이 몇개 필요한지 부터 시작해서 \(2^{n-1}\) 의 갯수, \(2^{n-2}\) 의 갯수… 이렇게 차례대로 갯수를 적어주면 된다. 한자리씩 내려올 수록 나누기 2를 하는 것과 같다.

이렇게 쭉 진행해 나가다가 0이하의 수로 떨어지면 그때부턴 \(2^-1\)(10진수로 0.5)이 제일 큰 단위가 된다. 이때부턴 한 자리씩 내려올 수록 \(\times 2\)를 하는 것과 같다.

✍️ 소수 부분이란 1보다 작은 수를 의미한다. 즉, 2진수 변환 결과 \(2^0\) 자리 아래쪽 자리를 의미한다. (\(2^{-1}, 2^{-2}, …\))

예를들어, 0.375를 2진수로 변환해보자.

  ∣  0.375 * 2 = 0.75  --> 0 (2^-1 의 자리)
  ∣  0.75 * 2  = 1.5   --> 1 (2^-2 의 자리)
  ∣  0.5 * 2   = 1.0   --> 1 (2^-3 의 자리)
  v  0 이므로 계산 종료
     => 0.011(2진수)

소숫점 아래 제일 큰 단위인 \(2^-1\) 이 0개, 그 다음 단위인 \(2^{-2}\) 가 1개, \(2^{-3}\) 이 1개가 된다. \[2^{-1} \times \color{red} 0 \color{black} + 2^{-2} \times \color{red} 1 \color{black} + 2^{-3} \times \color{red} 1 \color{black} = 0.011_2\] 이제 소수점을 2진수로 변환했으니 이대로 메모리에 저장하기만 하면 될까?

아래의 예시도 살펴보자.

    ex) 0.127  
 ∣  0.127 * 2 = 0.254 --> 0
 ∣  0.254 * 2 = 0.508 --> 0
 ∣  0.508 * 2 = 1.016 --> 1
 ∣  0.016 * 2 = 0.032 --> 0
 ∣  0.032 * 2 = 0.064 --> 0
 ∣  0.064 * 2 = 0.128 --> 0
 ∣  0.128 * 2 = 0.256 --> 0
 ∣  0.256 * 2 = 0.512 --> 0
 ∣  0.512 * 2 = 1.024 --> 1
 v  0.024 * 2 = 0.048 --> 0
  ....

위 예시처럼 아무리 2를 곱해도 소수점 아래가 0이 안나오는 경우도 있다. 즉, 숫자마다 2진수로 변환시 저장해야할 비트의 길이가 달라진다.

1. 고정소수점 방식(Fixed-point)

고정소수점 방식으로 2진수를 저장하게 되는 경우 그대로 저장한다.
\(12.375 = 1100.011_2\) 를 16bit 메모리 고정소수점 방식으로 저장한다면 아래 그림처럼 저장된다.

아주 직관적으로 2진수 변환 결과 그대로 메모리에 저장한다.

• 장점
  • 구현하기 쉽다.
  • 정수형 자료형의 연산은 부동소수점 자료형의 연산보다 빠르게 할 수 있다는 장점이 있다.
• 단점
  • 사용하는 비트 수 대비 표현 가능한 수의 범위 또는 정밀도가 낮다.
• 차이
  • 연산 절차 상으로는 부동소수점은 곱셈이 간편하고, 고정 소수점은 덧셈/뺄셈이 간편하다는 차이를 보인다.

2. 부동소수점 방식(Floating-point)

부동소수점 방식은 수를 \((가수) \times (밑수)^{(지수)}\) 와 같이 곱셈 형태로 표현한다. 예를 들어 12.375 의 경우 소수점 윗 부분을 2진수로 변환하면 \((12.)_{10} = (1100)_{2}\) 이고, 소수점 아래 부분을 변환하면 \((.375)_{10} = (0.011)_2\) 이 된다.

  // 정수부
  12
  = 1100
  
  // 소수부
  0.375
  = 0.375 * 2 = 0.75 -> 0
  = 0.75 * 2 = 1.5 -> 1
  = 0.5 * 2 = 1.0 -> 1
  
  // 결과
  12.375
  = 1100.011(2)

그 후 다음과 같이 세 부분의 값으로 실수를 저장한다.

• 부호부 (1비트) : 양수일 때는 0, 음수일 때는 1
• 지수부 (부호가 없는 정수, 8비트) : 8비트로 표시
• 정규화된 가수부 (부호가 없는 정수, 23비트) : 제일 앞의 비트는 정규화되었으므로 1이다.

정규화

먼저 정규화를 진행한다. 여기서 말하는 정규화란

  1.xxxx...* 2^n

의 형태로 나타내는 것을 말한다. 정수부에 1이 남을때 까지 소수점을 이동시켜 만든다.

  1100.011 -> 1.100011 * 2^3

위 정규화된 가수부 저장 방식대로 가수부에 그대로 저장한다. 남은 부분은 0으로 채운다.

지수부 저장

지수부 3을 IEEE 754 에 따라서 변경한다.
32bit 메모리에서 지수부 영역의 비트 수는 8bit 이므로 bias 값은 127이된다. bias 값을 더하는 이유는 지수가 음수가 되는 경우가 있기 때문이다.

  0.000101(2) -> 1.01 * 2^-4

이와 같이 지수가 음수가 되는 경우에도 8bit 영역으로 표시가 가능해야 한다. 이에 대한 아이디어로 8bit 영역을 반으로 나눠 음수와 양수로 표현한다는 것이다. 10진수 기준으로 0~127 구간을 음수로, 128~255 구간은 양수를 표현하게 한다. \(K(bias) = 2^{(8-1)} - 1 = 2^7 - 1 = 127\) 을 지수에 더해 130으로 만든 후 130을 2진수로 표현해 지수부에 저장한다.

  130
  = 1000 0010(2)

최종적으로 다음과 같이 저장된다. \(12.375 = 1100.011_2\)

정확도

이렇게 부동소수점을 사용했음에도 해결하지 못하는 문제가 있다. 소수 부분을 2진수로 변환할 때 그 길이를 미리 알 수 없다는 것이다. 즉, 32bit 의 경우(단정밀도) 23bit 에 해당하는 가수부 영역이 있지만 소수 부분의 가수부가 그 영역을 넘어갈 수 있다. 이럴 경우를 대비해 64bit(배정밀도) 체계를 지원한다. 64bit(배정밀도)

64bit(배정밀도) 에서는 지수부가 11bit 이고, 가수부가 52bit 로 32bit(단정밀도)에 비해 넉넉하다.

• 부호부 (1비트) : 양수일 때는 0, 음수일 때는 1
• 지수부 (부호가 없는 정수, 11비트) : 11비트로 표시
• 정규화된 가수부 (부호가 없는 정수, 52비트) : 제일 앞의 비트는 정규화되었으므로 1이다.
• \(K(bias) = 2^{11-1} - 1 = 1024 - 1 = 1023\)
• 0~1023 : 음수, 1024~2047: 양수

정리

java 에서는 부동소수점 저장 형식으로 float(32bit) 와 double(64bit) 가 존재한다.
소수점 연산을 정밀하게 저장해야 하는 경우 사용한다.

어떤 수의 자릿수(유효숫자)가 7자리 이하인 경우엔 높은 확률로 float(32bit) 에 저장될 수 있고, 15자리 이상인 경우 double(64bit) 에 저장해야 그나마 정확한 숫자를 저장할 수 있다.

reference

• https://gsmesie692.tistory.com/94
• https://ko.wikipedia.org/wiki/부동소수점
• Inpa Dev님 블로그